FUNCIONES DISCRETAS
Una función discreta 
es una funcion matematica cuyo dominio y codominio están contenidos en 
, es decir, es una función:
El dominio de estas funciones es un conjunto discreto, y por tratarse de una funcion su conjunto imagen también lo es.
Graficas de las Funciones Discretas:
- Binomial
- Poisson
- Geometrica
- Hipergéometrica
BINOMIAL:
Una distribución binomial es una distribución de probabilidaddiscreta que mide el número de éxitos en una secuencia de n ensayos independientes de Bernoulli con una probabilidad fija p de ocurrencia del éxito entre los ensayos.
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Formula de la Distribucion Binomial:
Donde:
- n es el número de pruebas.
- k es el número de éxitos.
- p es la probabilidad de éxito.
- q es la probabilidad de fracaso.
Aplicando la formula anterior a una serie de valores aleatorios, obtenemos la siguiente grafica de distribucion binomial:
DISTRIBUCION DE POISSON
La distribución de Poisson es discreta (como la binomial) pues los valores que puede tomar la variable aleatoria son números naturales. Aunque en la distribución de Poisson los casos posibles en teoría son infinitos (numerable).
La distribución de Poisson se caracteriza por un solo parámetro landa. Su media es landa y su varianza también es landa.
La distribución de Poisson tiene la siguiente forma matemática:
donde:
- Px representa la probabilidad de ocurrencia de x individuos en una cuadrícula.
- m (mu) es la media poblacional del número de individuos en una cuadrícula.
Aplicando la formula anterior a una serie de numeros aleatorios, se produce la siguiente grafica:
DISTRIBUCION GEOMETRICA
En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabiliad discretas siguientes:
- la distribución de probabilidad del número X del ensayo de Benoulli necesaria para obtener un éxito, contenido en el conjunto { 1, 2, 3,...} o
- la distribución de probabilidad del número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1, 2, 3,... }.
Cual de éstas es la que uno llama "la" distribución geométrica, es una cuestión de convención y conveniencia.
Si la probabilidad de éxito en cada ensayo es
p, entonces la probabilidad de que
x ensayos sean necesarios para obtener un éxito es:
para
x = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya
x fallos antes del primer éxito es:
para x = 0,1, 2, 3,....
En ambos casos, la secuencia de probabilidades es una progresión geometrica.
El valor esperado de una variable aleatoria X distribuida geométricamente es:
y dado que Y = X-1,
En ambos casos, la varianza es:
Las funciones generatrices de probabilidad de X y la de Y son, respectivamente,
Aplicando la formula anterior a una serie de valores aleatorios obtenemos la siguiente grafica de distribucion geometrica:
DISTRIBUCION HIPERGEOMETRICA
En teoría de la probabilidad la
distribución hipergeométrica es una distribucion discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de
N elementos de los cuales,
dpertenecen a la categoría
A y
N-d a la
B. La distribución hipergeométrica mide la probabilidad de obtener
x (
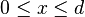
) elementos de la categoría
A en una muestra de
n elementos de la población original.
La función de probabilidad de una variable aleatoria con distribución hipergeométrica puede deducirse a través de razonamientos combinatorios y es igual a:
donde
N es el tamaño de población,
n es el tamaño de la muestra extraída,
d es el número de elementos en la población original que pertenecen a la categoría deseada y
x es el número de elementos en la muestra que pertenecen a dicha categoría. La notación
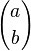
hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar
b elementos de un total
a.
El
valor esperado de una variable aleatoria
X que sigue la distribución hipergeométrica es:
Y su varianza es:
Aplicando la formula anterior a una serie de numeros aleatorios se obtiene la siguiente grafica de distribucion hipergeometrica:
